On this site I write about, what I like to believe is, a diverse set of topics. The normal way of presenting posts using a sequential list does nothing to help people discover other material on the site which they may also be interested in. I wanted to provide visitors with a list of links to content which is similar to the page they are currently viewing. However, due to limitations in the platform I’m using, there was no option to simply turn this on. So, I wrote some code and implemented an algorithm to solve this problem.
This blog is published using a static site generator called Jekyll. It offers a site variable which provides a list of related posts, but that feature has two modes. If Jekyll is started with the appropriate command, then the feature uses latent semantic indexing (LSI) to determine actual similarity between posts. However, the default behavior is to simply provide the ten most recent posts, which doesn’t seem all that useful. Its main use is probably being a fallback method for providing results when the LSI method is not available. Github pages, where this site is hosted, only uses the default behavior. People have found creative ways to simulate more sophisticated matching, such as looking at tag or category similarity to find related documents in Jekyll. But, I don’t want to worry about tagging posts in a way that their site can semi-automatically correlate the pages. I just want related pages to be automatically linked without me thinking about the appropriate tags to use.
Since using a Jekyll plugin to accomplish this is not possible, the next best thing is to create a script which can run after new posts are created. If it was fast enough a git post-commit hook could be created to run it automatically after new content is committed. So, a small script is just needed to extract the page contents and perform latent semantic analysis (LSA) on the data.
I could probably look at the Jekyll codebase and extract the code which they have to perform latent semantic indexing (LSI). But, I have done this before, so I decided to it would be fun to roll my own. As we get into the details of what makes this work, we will talk about the math that makes it possible. There will be few formulas, but plenty of tables, so hang in there. You can do this!
The content from each post will get extracted from the markup, and every word on the site will be put into a dictionary. Then, a matrix will be created which lists all of the documents and the number of times the document contains each word in the dictionary.
| word 1 | word 2 | word 3 | word 4 | word 5 | |
|---|---|---|---|---|---|
| document 1 | 1 | 3 | 0 | 0 | 0 |
| document 2 | 0 | 2 | 1 | 0 | 0 |
| document 3 | 0 | 0 | 2 | 2 | 0 |
| document 4 | 0 | 0 | 0 | 1 | 1 |
We could try to look at the similarity between a pair of documents by measuring how far apart they are in terms of words. For example, document 1 has 3 occurrences of word 2 and document 2 has 2 occurrence of word 2, so maybe this means they have something in common. That task quickly becomes impossible to do in your head as the number of documents and words increases. A mathematical technique is needed. Since each row in this matrix can be seen as a vector, we could measure the distance between word vectors using Euclidean distance. That sounds fancy, but it just means extending the Pythagorean formula which you likely know (a² + b² = c² ≝ c = √(a² + b²)) from 2-dimensions to n-dimensions (c = √(a² + b² + … + n²)).
Taking that approach would probably work to some extent, but it would be susceptible to noise in the raw data. Words which have little importance to the overall meaning of the document would get the same weight as more important words. That technique also wouldn’t provide any additional insight into hidden relationships present in the data. The matrix needs to be broken into components so that there’s a chance to reduce the impact of components which contribute noise and a chance to find hidden relationships. The mathematical process to factor a matrix is called singular value decomposition. Through this process the original matrix M will be broken down into three new matrices: U, Σ, and Vᵗ (i.e. M = UΣVᵗ).
Matrix U has all of the original documents, but the documents are no longer described in terms of words. The columns represent different combinations of the underlying words. If we pretend for a minute that the documents are paintings and that the words represent colors, we might be able to say that column 1 in matrix U represents how purple, for example, each of the documents is. If word one of matrix M was red and word two of matrix M was blue, then 1 in matrix U may be representing some combination of word one and word two in the original matrix (red and blue mix to form purple).
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| document 1 | 0.80260058 | 0.27111885 | -0.25574933 | -0.46574580 |
| document 2 | 0.56405355 | -0.05780625 | 0.35693728 | 0.74235962 |
| document 3 | 0.19155285 | -0.92089692 | 0.16510959 | -0.29663983 |
| document 4 | 0.03135919 | -0.27404719 | -0.88313469 | 0.37945732 |
Matrix Σ is a diagonal matrix which contains what are known as singular values. These values essentially represent how strong each of the factors are. In this example the first singular value (3.77050319) is five times as influential as the final singular value (0.66068518).
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 3.77050319 | 0 | 0 | 0 | 0 |
| 0 | 2.95308616 | 0 | 0 | 0 |
| 0 | 0 | 1.27517955 | 0 | 0 |
| 0 | 0 | 0 | 0.66068518 | 0 |
In this case we may be able to discard the last two singular values, as well the corresponding values in matrices U and V, and not loose much useful information. There is a good chance that those less influential singular values represent the noise in the data set.
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 3.77050319 | 0 | 0 | 0 | 0 |
| 0 | 2.95308616 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
The final script discards all singular values after a 50% drop is detected; column 3 (1.27517955) would need to be at least 1.476545 or greater to be included in the results. Since those values are changing to zeros, and due to how matrix multiplication works, it is also possible reduce the size of matrices U and Vᵗ. Columns 3 and 4 of matrix U, and rows 3 through 5 of matrix Vᵗ can be dropped. Dropping those columns and rows reduces the amount of memory required by the program, and it reduces the computation time by eliminating calculations which we know will all equal zero.
Matrix Vᵗ (V transpose) is very similar to matrix U. The main difference is that it is from the perspective of words rather than documents. If we did not transpose the matrix, then the words would be in the left header column, just like the documents are in matrix U. For the use case of finding document similarity we are looking at things in terms of documents – what is the similarity between documents – so, we will not need to use matrix Vᵗ.
| word 1 | word 2 | word 3 | word 4 | word 5 | |
|---|---|---|---|---|---|
| 1 | 0.21286299 | 0.93778169 | 0.25120235 | 0.10992296 | 0.00831698 |
| 2 | 0.09180865 | 0.23627623 | -0.64325929 | -0.71648469 | -0.09280027 |
| 3 | -0.20055947 | -0.04185562 | 0.53887035 | -0.43359817 | -0.69255713 |
| 4 | -0.70494362 | 0.13241076 | 0.22564448 | -0.32363725 | 0.57433908 |
| 5 | 0.63960215 | -0.21320072 | 0.42640143 | -0.42640143 | 0.42640143 |
With our document matrix decomposed, we can put it back together with just the components that are likely to provide valuable insights. Those insights were not visible, or latent, in the original matrix. Combine that with the fact that we are looking for language related, or semantic, insights, and you see where the name of this technique comes from.
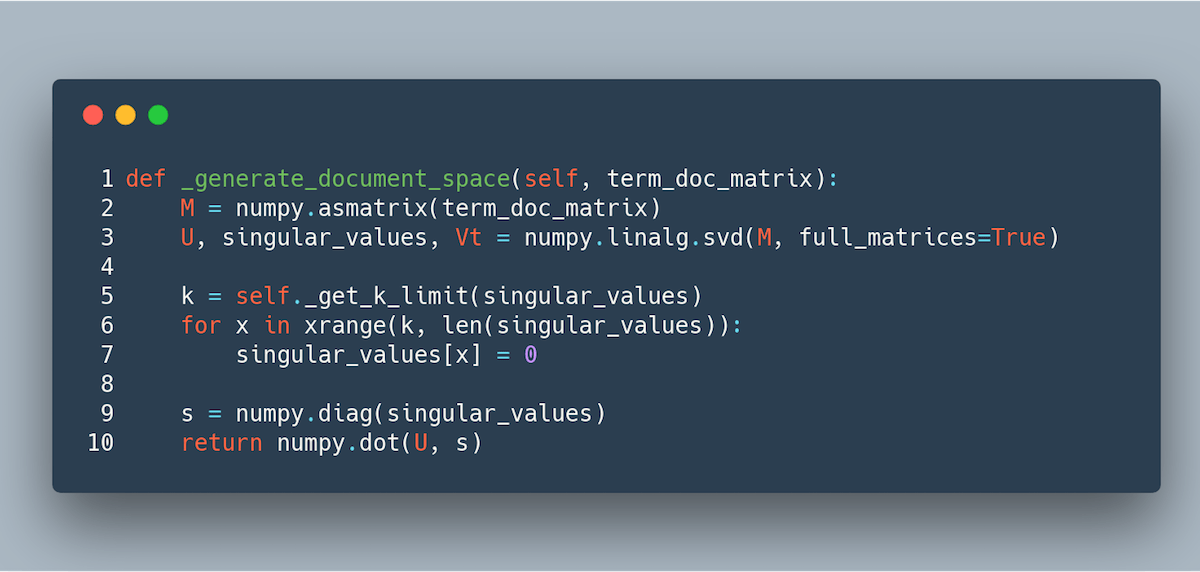
Matrix U is document-centric, so we will use that matrix along with our singular values to generate our search space, or document space. Recomposing the data is as simple as taking the dot product of matrix Σ and matrix U.
| 1 | 2 | |
|---|---|---|
| document 1 | 3.02620806 | 0.80063732 |
| document 2 | 2.12676573 | -0.17070684 |
| document 3 | 0.72225062 | -2.71948796 |
| document 4 | 0.11823994 | -0.80928496 |
All documents are listed in the document concept space; the words have been approximated in fewer dimensions. Because we have reduced our space into just two dimensions we can easily visualize it with a simple graph. We are plotting lines rather than points because these are vectors. The documents are ordered clock-wise; document 1 is blue and document 4 is teal. This arrangement makes sense given the ordered and overlapping nature of the original data.
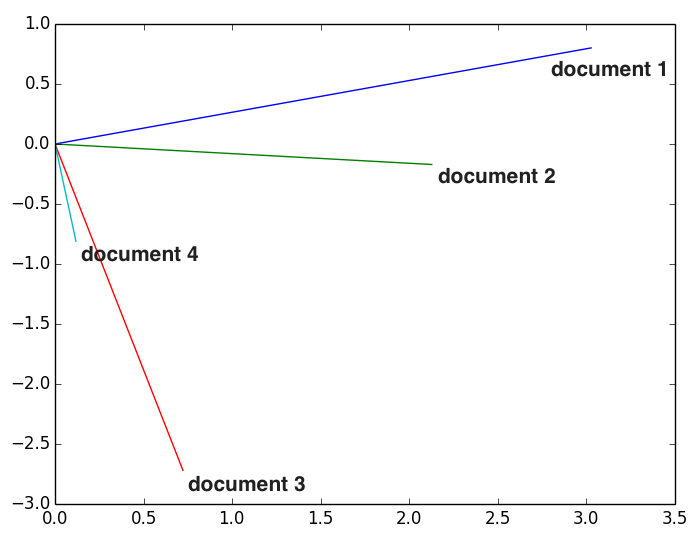
Since the body of our original matrix contained word counts and similarity of word counts is unlikely to help identify the similarity of documents, we do not want to factor the magnitude of any dimension into our similarity calculation. Because we want to ignore the magnitude, we do not want to use Euclidean distance as our measure. Instead we will use cosine similarity which measures the angle between the vectors. The angles separating the vectors in the figure above seem to match what we would expect the similarity to be based upon how words show up in the documents. The original document-word matrix is show below.
| word 1 | word 2 | word 3 | word 4 | word 5 | |
|---|---|---|---|---|---|
| document 1 | 1 | 3 | 0 | 0 | 0 |
| document 2 | 0 | 2 | 1 | 0 | 0 |
| document 3 | 0 | 0 | 2 | 2 | 0 |
| document 4 | 0 | 0 | 0 | 1 | 1 |
To calculate cosine similarity, two documents are first chosen. A numerator is created by performing a dimension-wise multiplication of the document vectors and then summing the individual values. If document 1 was compared to document 2, the numerator would be: (3.02620806 * 2.12676573) + (0.80063732 * -0.17070684) = 6.299361327. A denominator is created by squaring the sum of each dimension of a document vector, taking the square root, and multiplying that by the square-rooted sum of each dimension of the other document vector. For the case where document 1 was compared to document 2, the denominator would be: √(3.02620806² + 0.80063732²) * √(2.12676573² + -0.17070684²) = 6.6788863384. The final score would be 6.299361327 ÷ 6.6788863384 = 0.943175405. The range of the cosine function is -1 to 1, so that score indicates similarity.
With that, the hard part is complete. Now, for each document which requires associated documents, we just find its entry in this space and calculate the cosine distance to every other document in the space. We take the top n matches (dropping the number one match, which should be the document itself), and those are the most semantically similar documents. Easy.
Below is the code to accomplish all of this. It is an early beta – pretty much everything is hard-coded. To determine which pages should get related posts and where the related posts section should go, I just search for any instance of a div tag with id="related" and class="clearfix". The results of this technique are currently being used on the site though. Presently, related pages are listed at the bottom of posts, below the code excerpt on this page.
The screenshot in this post is courtesy of carbon.